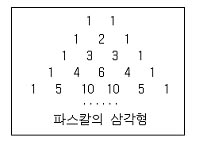
▲파스칼 삼각형 ⓒ 이태욱
아마 '파스칼의 삼각형'을 아는 사람이라면 이 문제를 쉽게 해결했을 것이다. 파스칼의 삼각형이란 양끝에 1이라는 숫자를 넣고 위의 두 수를 아래로 더해가는 형태의 수열이다. 이 수열은 '인간은 생각하는 갈대'라는 문구로 유명한 책 <팡세>를 지은 철학자이자 수학자인 파스칼(Blaise Pascal, 1623~1662)에 의해 연구 발전됐다.
파스칼의 삼각형은 파스칼의 이름을 땄으나 기본적인 원리는 파스칼에 의해 만들어진 것이 아니다. 이미 12세기에 중국과 페르시아에서 몇몇 산술적인 성질들이 알려져 있었다. 파스칼의 삼각형은 16세기와 17세기에 걸쳐 서유럽의 많은 수학자들의 연구에 등장했다.
파스칼은 1665년에 이 삼각형의 성질에 대한 연구 결과들을 발표했다. 특히 이러한 결과들을 그가 연구한 확률론에 많이 사용하였기에 파스칼의 이름이 붙여졌다. 모든 숫자를 앞에서 읽어도, 뒤에서 같은 숫자가 되는 이 수열은 확률의 이항정리에 많이 응용된다. 이항정리란 (a+b)ⁿ처럼 두 항을 더한 것의 거듭제곱을 전개하는 공식을 말한다.
파스칼의 삼각형은 이항정리의 계수들로 이루어진 자연수들의 특별한 배열을 나타낸다. 이 공식은 뉴턴의 묘비에 적혀 있을 만큼 유명한 정리이다.
다음 문제는 베르나르 베르베르의 유명한 소설 <개미>에 나오는 문제다. 1, 11, 12, 1121, 122111,112213, 12221131… 과 같이 계속되는 수열이 있다. 이 숫자들은 어떤 규칙을 가지고 순서대로 배열되어 있다. 다음에 나올 숫자는 무엇일까?
정답: 1123123111
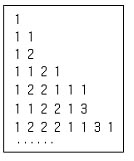
▲베르나르 베르베르 수열 ⓒ 이태욱
이는 첫 번째 숫자를 보고 '1이 하나'하고 읽은 것이 2번째 줄의 숫자이다. 2번째 숫자를 '1이 둘'하고 읽은 것이 세 번째 줄이다. 네 번째 줄은 세 번째 숫자를 보고 '1이 하나, 2가 하나'를 숫자로 적은 것이고 이런 식으로 마지막 줄의 숫자를 읽어 보면 '1이 하나, 2가 셋, 1이 둘, 3이 하나, 1이 하나'이므로 정답은 1123123111이다.
다음은 알파벳으로 나열한 문자열, 아니 숫자와 관련이 있으므로 그냥 수열이라고 하자. O, T, T, F, F, S, … 와 같이 배열되어 있는 수열에서 마지막 S 다음에 올 문자는 무엇일까?
정답: S
이 수열은 One, Two, Three, Four, Five, Six … 식으로 숫자를 읽고 영어 숫자들의 알파벳 첫 글자를 순서대로 늘어놓은 것이다. 따라서 7번째 Seven으로 S가 답이다.
이러한 문제는 재미는 있지만 일부 사람들은 의문을 제기하기도 하고 총기가 넘치는 사람은 더욱 기발한 답을 만들어 내기도 한다. 이러한 혼란을 막기 위해 여러가지 약속을 정한다. 더하기가 일정하면 등차수열, 곱하기가 일정하면 등비수열, 피보나치가 만든 피보나치수열, 티티누스가 만들어 낸 티티누스수열. 여러분도 자신만의 수열을 만들어 보아 수학사에 이름을 하나 올려보세요.